Although all IP addresses under IPv4 is going to be fully utilized in near future days, it will take a considerable period to transition the running networks on IP version 6. Consequently the concept of subnetting will remain at highest important place. With the advent of IP version 6, there will be no requirement to preserve the IP addresses by the means of subnetting but again it will take some years to get it into the market in full swing.
Understanding IPv4 Subnetting
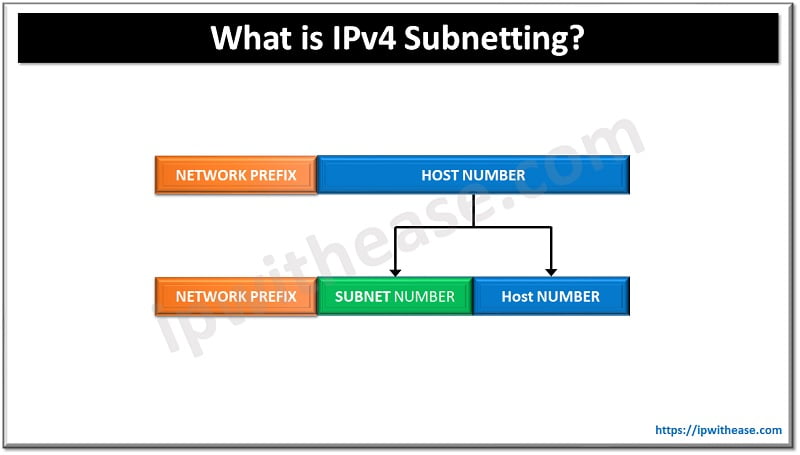
In subnetting we borrow few bits of host part in to network part so that we can have many small subnets and few hosts in each subnet to preserve IP addresses. For example- If we take a normal IP address pool 200.10.25.0/24 of class C, all the valid host IPs from 200.10.25.1 to 200.10.25.254 can be assigned to only one customer irrespective of the number of hosts required.
By subnetting we can divide this pool 200.10.25.1 to 200.10.25.254 into as many subnets as per the requirement of customers by assigning different subnet mask other than the default 255.255.255.0.
Formula for calculation of number of valid subnets
Formula for calculation of number of valid subnets is 2n-2 where n is the number of borrowed bits. Number of valid hosts per subnet can be calculated by 2n-2 where n is the number of host bits left. Magic number or subnet width can be calculated by deducting the interesting octet from 256.
Here I am trying to make this grueling concept as easy as it can be.
Let’s start with subnet mask as it’s a crucial part of subnetting.
Subnet Mask
Subnet mask gives an idea that how many bits out of assigned 32 bits address are used to represent network and how many for hosts.
Example-
IP Address – 10.1.0.0 Subnet mask-255.255.255.248 (In VLSM it can be written as 10.1.0.0/29)
Here 29 bits are assigned for the network part and only 3 bits are representing the host part.
The numeral value of 248 in the last octet of the IP address concludes that first 5 bits are “on” and so giving a numeral value of 248(i.e. 128+64+32+16+8=248). All the remaining “off” bits is used for the host part.
Note: In calculation of subnet mask, if a bit is “on” then its corresponding decimal number is added and in case of “off” state it’s not added. So the numeral values (i.e. 4, 2 & 1) of 6th, 7th & 8th bit are not added.
Examples of subnetting
(1) Take a Class C IP pool 200.10.5.25/26 or 200.10.5.25 255.255.255.192 of class C. Here we have borrowed 2 bits from host part as default bits for network in class C is 24 bits (i.e. 255.255.255.0).
By formula, the number of valid subnets is 22-2=2.
The number of valid hosts in each subnet is 26-2=62 as first IP address is fixed for network address and last IP is for broadcast address.
In first subnet the PCs can be assigned any IP from 200.10.5.65 to 200.10.5.126.
Note: Here the interesting octet is the fourth octet as it has subnet mask (i.e. 192) rather than 255. So we see no changes in 200.10.5.
Practical benefit:-If two customers come to a provider with a demand of 60 hosts IPs each, we can assign 200.10.5.64/26 to first & 200.10.5.128/26 to second. Without subnetting we would have to assign the entire pool of 200.10.5.0/24 to one and 200.10.x.0/24 to other and it would be a loss of more than 200 IPs.
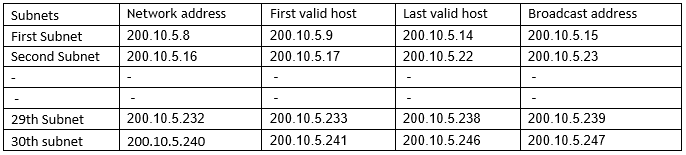
(2) Take IP pool 200.10.5.16/29 or 200.10.5.16 255.255.255.248 of class C. Here 5 bits are borrowed from host part.
Number of valid subnets=25 -2 = 30
Number of valid hosts per subnets=23 – 2=6
(3) Take IP pool 160.40.60.5/19 or 160.40.60.5 255.255.224.0 of class B. As the default subnet mask of class B is 255.255.0.0 (or /16) so the interesting octet here is the third octet which is 224. Hence all the subnets will have 160.40 parts common. Here we have borrowed 3 bits from host part.
Number of valid subnets=23-2=6
Number of valid hosts per subnet=213-2=8190
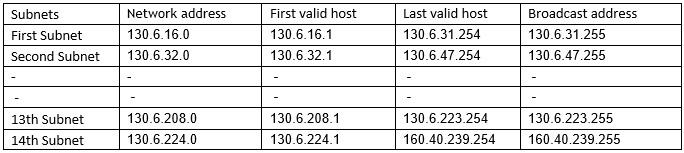
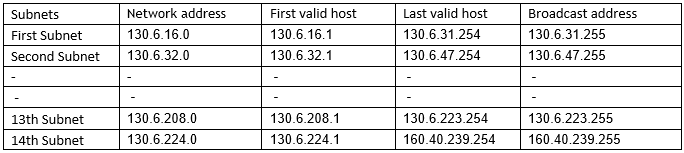
(4) Take IP pool 130.6.9.20/20 or 130.6.9.20 255.255.240.0. Here 4 bits from host bits are borrowed and interesting octet is third octet. Means all subnets will have 130.6 parts common.
Number of valid subnets=24-2=14
Number of valid hosts per subnet=212 -2=4094
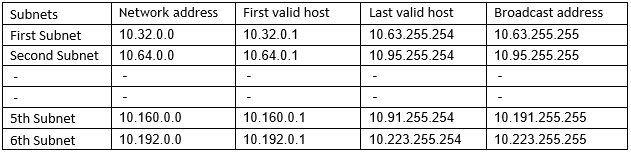
(5) Take an IP pool of class A 10.10.0.5/11 or 10.10.10.5 255.224.0.0. Here 3 bits are borrowed as class A has default subnet mask of 255.0.0.0. Class A gives the maximum number of valid host IPs.
Number of valid subnets=23-2=6
Number of valid hosts per subnets=221-2=2097150
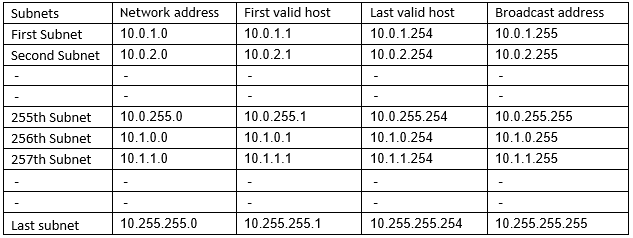
(6) Take another class A IP pool 10.0.0.0/24 or 10.0.0.0 255.255.255.0 (We are using this for one of our cream customerJ). Here 16 bits are borrowed from host part in to network part.
Number of valid subnets=216-2=65534
Number of valid hosts per subnet=28-2=254
Note: By using “ip subnet-zero” command in global configuration mode we can use the first and last subnets also which we didn’t use in above examples. With “ip subnet-zero” command the number of subnets is 2n rather than 2n-2 but there is no change in the formula of valid hosts.
Continue Reading:
Meaning of Ping Response for IPv4 Address
ABOUT THE AUTHOR

You can learn more about her on her linkedin profile – Rashmi Bhardwaj